Top 10 Low Pass Filter Techniques for Better Signal Processing
In the realm of signal processing, the significance of Low Pass Filters (LPFs) cannot be overstated. As the demand for high-quality audio and data processing rises, industries are increasingly relying on LPF techniques to eliminate unwanted high-frequency noise and enhance the clarity of signals. According to a recent market research report by Allied Market Research, the global low-pass filter market is projected to reach $1.6 billion by 2027, growing at a compound annual growth rate (CAGR) of 5.2% from 2020 to 2027. This rise underscores the critical role that LPFs play in various applications, from telecommunications to consumer electronics.
Expert in the field, Dr. Jane Roberts, a renowned signal processing engineer, emphasizes the importance of LPFs, stating, "A well-designed Low Pass Filter is essential for maintaining signal integrity and optimizing performance in every digital system." As such, exploring the top LPF techniques not only equips engineers with the necessary tools for effective signal management but also contributes to the ongoing evolution of technology across multiple sectors. This article delves into the ten best Low Pass Filter techniques, showcasing their applications and advantages in achieving superior signal processing outcomes.
Understanding Low Pass Filters and Their Importance in Signal Processing
Low pass filters (LPFs) play a crucial role in signal processing by allowing low-frequency signals to pass through while attenuating higher frequencies. This selective filtering is essential in various applications, including audio engineering, telecommunications, and image processing. By removing unwanted high-frequency noise, LPFs enhance the clarity of the desired signal, making them indispensable tools for both engineers and researchers.
The importance of low pass filters extends beyond mere noise reduction. They are vital in smoothing out data, facilitating better analysis and interpretation of signals. For instance, in digital signal processing, LPFs can help eliminate aliasing effects during sampling, ensuring that the final output accurately represents the original signal. Additionally, they are integral in maintaining signal integrity during transmission, preventing distortion and ensuring that the receiver captures a clean and coherent signal. By understanding these two principal roles of low pass filters—noise reduction and signal integrity—professionals in the field can make informed decisions when selecting and implementing filtering techniques in their projects.
Top 10 Low Pass Filter Techniques for Better Signal Processing
| Filter Technique |
Cutoff Frequency (Hz) |
Order |
Ripple (dB) |
Application |
| Butterworth |
1000 |
4 |
0.5 |
Audio Processing |
| Chebyshev |
2000 |
3 |
1.0 |
Signal Conditioning |
| Bessel |
1500 |
2 |
N/A |
Phase Response |
| Elliptic |
2500 |
5 |
0.5 |
Telecommunications |
| Gaussian |
1800 |
4 |
N/A |
Data Smoothing |
| Mean |
Variable |
N/A |
N/A |
Simple Averaging |
| Moving Average |
Variable |
N/A |
N/A |
Time Series Analysis |
| Savitzky-Golay |
Variable |
Polynomial Order |
N/A |
Spectral Analysis |
| Kalman Filter |
Variable |
N/A |
N/A |
Navigation Systems |
Common Applications of Low Pass Filters in Electronic Systems
Low pass filters (LPFs) are essential components in electronic systems, serving various applications that require the suppression of high-frequency noise while allowing low-frequency signals to pass through. One of the most common applications of LPFs is in audio processing, where they help eliminate unwanted high-frequency hum and hiss, ensuring that the audio output remains clean and clear. By filtering out these higher frequencies, LPFs enhance the listening experience in devices such as mixers, amplifiers, and consumer audio equipment.
Another significant application of low pass filters is in data acquisition systems, where they play a crucial role in signal conditioning. In environments where measurements may be contaminated by high-frequency interference, LPFs help improve the integrity of the data collected from sensors. This is particularly important in fields like industrial automation and biomedical monitoring, where accurate readings are vital for system performance and safety. By smoothing out the signal, LPFs ensure that the information conveyed is representative of the actual physical phenomena being monitored, thereby promoting better decision-making based on the processed data.
Overview of the Top 10 Low Pass Filter Techniques
Low pass filters (LPFs) play a crucial role in signal processing by allowing low-frequency signals to pass while attenuating higher-frequency noise. There are various techniques for implementing low pass filters, each with unique characteristics suited for different applications.
Among the most popular methods are the Butterworth filter, known for its maximally flat frequency response; the Chebyshev filter, which allows for ripple in the passband but provides a steeper roll-off; and the Bessel filter, which offers a smooth response ideal for applications requiring minimal phase distortion.
In addition, digital techniques such as moving average filters and first-order FIR filters offer flexible, easy-to-implement options for low pass filtering in digital signal processing environments. For more advanced needs, the use of wavelet transforms has gained popularity; these allow for adaptive filtering based on the frequency characteristics of the incoming signal. Analog solutions, like the Sallen-Key topology, provide efficient low pass filtering with minimal component count. Each of these techniques serves specific requirements, and selecting the appropriate one depends on the desired filter characteristics, such as bandwidth, sharpness of cut-off, and computational efficiency.
Detailed Analysis of Each Technique: Advantages and Disadvantages
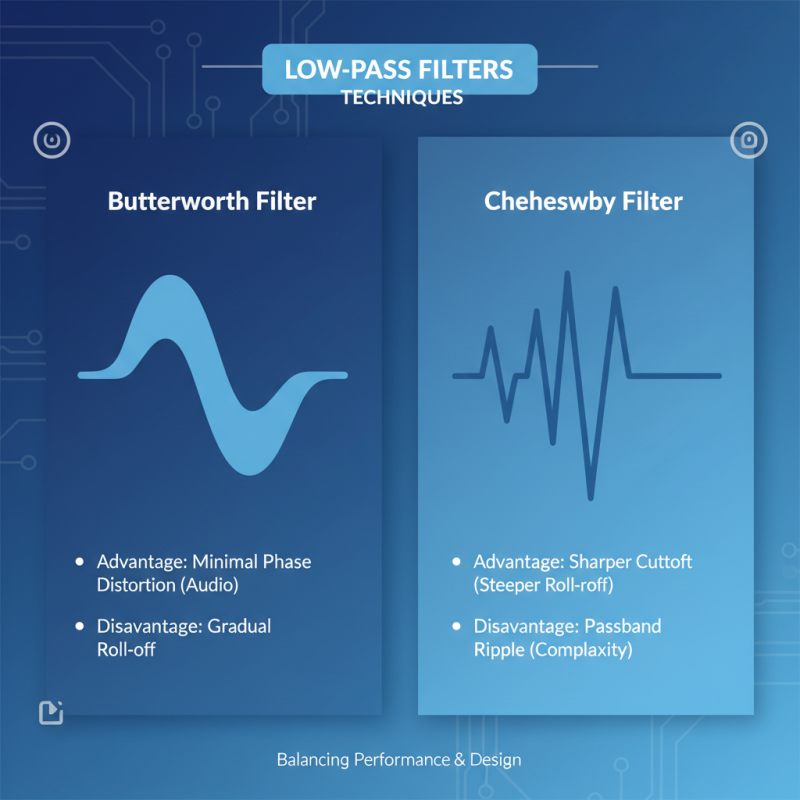
When considering low pass filter techniques, it's essential to weigh their advantages and disadvantages for effective signal processing. One common method is the Butterworth filter, known for its smooth frequency response. The primary advantage is minimal phase distortion, making it ideal for audio applications; however, it may not perform as well in steeper roll-offs compared to other filters. Another technique is the Chebyshev filter, which offers a sharper cutoff frequency at the expense of some passband ripple. This can be beneficial when the priority is to minimize unwanted high-frequency signals, but the trade-off can lead to increased complexity in the design.
Tips for implementation: Always simulate the filter design using software tools to evaluate performance under various conditions. This can help identify potential issues early, ensuring that your chosen technique meets your project's requirements. Additionally, consider the computational resources available; some techniques might require more processing power, which could be a limiting factor in real-time applications. For systems where latency is critical, simpler filters may offer sufficient performance without the added complexity and delay of advanced methods.
Best Practices for Implementing Low Pass Filters in Signal Processing
When it comes to implementing low pass filters in signal processing, adhering to best practices is essential for achieving optimal results. A low pass filter allows signals with a frequency lower than a certain cutoff frequency to pass through while attenuating higher frequencies, which is crucial for noise reduction and signal clarity. One key aspect is selecting the appropriate type of low pass filter, whether it be a simple first-order filter or a more complex higher-order filter. Understanding the characteristics of different filter designs can significantly impact the performance and reliability of your signal processing tasks.
Tips for implementation include ensuring that your cutoff frequency is set correctly based on the characteristics of the signal you are filtering. This requires a thorough analysis of the signal's frequency spectrum. Additionally, consider the filter's roll-off rate, as a steeper roll-off can lead to signal distortion. It's also advisable to test the filter’s performance using simulated data before applying it to real-world signals, allowing for adjustments without risking data integrity.
Furthermore, be mindful of the computational resources required for implementing complex filtering techniques. Simpler filters often require less processing power and can be more suitable for real-time applications. Lastly, ensure that your filter design maintains the necessary phase response for your applications, as this can influence the temporal accuracy of the signals post-filtering. By following these best practices, you'll enhance your signal processing capabilities and achieve clearer, more reliable outputs.
